 por javierfl » Dom Ene 08, 2012 5:27 pm
por javierfl » Dom Ene 08, 2012 5:27 pm
Muy interesante el análisis y una muestra de como muchas de las físicas del material que anda por ahí están hechas un tanto al tuntún.
Una cosa que aún me causa muchas dudas es el tema del nivel del agua. Suponía que el nivel de agua era la proporción entre volumen de caldera y volumen de agua no vaporizada, es decir que el máximo de agua en la caldera sería 1 (caldera llena), siendo el óptimo entre el 0.6 y 0.8 más o menos, para dejar la correspondiente cámara de vapor. Sin embargo veo ( y así lo he comprobado) que en RW se usa un valor de1.25. Obviamente este valor no puede referirse a la proporción que digo porque significaría que hay más agua que volumen de caldera. Sólo puede referirse a la altura del agua en el tubo de nivel, pero no tengo ni idea de como se implementa u opera este importantisimo valor en ese caso, aunque es cierto que tampoco lo he investigado mucho aún. ¿Alguna idea?.
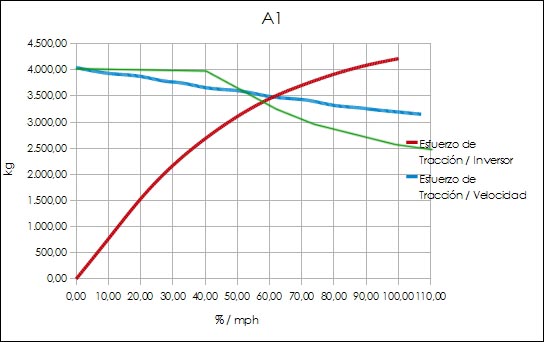
Respecto de las curvas, bien en realidad el simulador no reproduce (sería imposible) todas las variables de la realidad ni por tanto las curvas son equivalentes. El problema por explicarlo brevemente, es que en una locomotora real se obtiene el máximo esfuerzo de tracción con la admisión abierta a tope, y aquél se podría mantendría constante si no fuera preciso reducir la admisión porque con el aumento de velocidad (y por tanto de los ciclos de entrada y salida de vapor) llega un momento en que el vapor literalmente no es suficiente para trabajar en el cilindro. Por lo tanto, a partir de determinada velocidad se ha de reducir la admisión, lo que obviamente supone menos vapor trabajando y una reducción de dicho esfuerzo, que decrece hasta la velocidad límite. Aún asi se puede mover el tren porque en la práctica se ve compensado de alguna manera por la inercia. Después habría que considerar como variables, como afecta la mayor velocidad ( y por lo tanto el escape) a la capacidad de producción horaria de la caldera, como la velocidad afecta al rendimiento mecánico de la máquina, el tipo de distribución, la adherencia, las rampas y mil cosas.
Dentro de la simplificación de variables y curvas que obviamente se usa en RW el gráfico de la A1 es razonablemente correcto, aunque la mezcla de valores de admisión y velocidad en las X en el mismo gráfico es un poco rara. Esto viene dado, probablemente, porque en RW se tienen a bajar admisión demasiado pronto. Por ello, en vez de la línea azul, con esfuerzo de tracción constante hasta una velocidad dada cabría admitir la línea verde que adjunto, con la palanca abierta a tope hasta mayor velocidad y por tanto un esfuerzo de tracción constante ella. La implantación práctica de esto choca con el sistema de variables de RW y por lo tanto es complejo de implementar, sin que posiblemente tampoco varíe el realismo.
En todo este tema parto, obviamente, de que no es lo mismo esfuerzo de tracción, que se mide normalmente en Kg, de la potencia, que se mide en caballos. El esfuerzo de tracción es un valor en el gancho y la potencia la capacidad teórica desarrollada por la máquina. Una máquina puede desarrollar una potencia teórica elevada pero tener un esfuerzo de tracción relativamente pequeño si, por ejemplo, tiene poca adherencia, tiene gran rozamiento en el rodaje, gran resistencia aerodinámica, su mecanismo no es eficaz, etc. Esto se entiende perfectamente si se considera un ejemplo: dos caballos de la misma fuerza (un caballo cada uno...) tienen que arrastrar un carro sobre un empedrado mojado, uno tiene herraduras de hierro y el otro de goma. Aunque su potencia (1 CV) sea la misma, el que las lleva de goma, merced a su mayor adherencia, va a poder arrastrar más peso en kilos en el carro (lo que puede traccionar o esfuerzo de tracción) que el otro, que patinará sobre el suelo.
RW usa ambas variables, potencia (Power) y esfuerzo de tracción (Power).
Respecto a como considera RW estas unidades, este es uno de los problemas que más quebraderos de cabeza ha generado a los autores, porque son una mezcolanza de sistemas. resumo mis conclusiones al respecto:
Max Power:
Es la máxima potencia teórica que desarrolla la locomotora. Se pone en los caballos que tenga lo que sea. Ya no sé si son HP británicos o métrico, pero la diferencia es muy pequeña. Los Developer Docs. hablan de ponerlo en kW (1 kW = 1,341 HP (ingleses)o 1 kW = 1,359 HP (métrica)) pero de hecho he visto que al menos en la EMD f7 y el la DB V200 ponen los caballos. En los blueprint se pone como unidad Horsepower, que creo es lo que es. Importante al ir a velocidad.
Evidentemente los 14.500 caballos de la BR 7MT está mal; probablemente es un error al trascribir el listado y el valor real es de 1.450 CV. Una Santa Fe de Renfe, las de mayor potencia y de las mayores de Europa, tenía "sólo" 2.700 Cv. Abona esto que el esfuerzo de tracción (32) consignado sí que se correponde al real de 32.150 lbf.
Max Force:
Es donde he tenido más problemas de identificar la unidad y como se determina en los blueprints y en las curvas. Es el máximo esfuerzo de tracción en el arranque. No confundir con el esfuerzo de tracción máximo a regimen continuo, que es el que se da a una velocidad determinada. Aquí se trata del esfuerzo de tracción más elevado, el del arranque.
Los Developer hablan de kN (!) indicando que un 1kN = 225lbf para despues señalar que es en kilowatios y sin embargo en el blueprint se pone como unidad lbf (libras de potencia). Al final, sin embargo, en todos los casos se ponen valores muy bajos. De eso y la lógica se llega a la conclusión de que en este caso usan valores en klbf es decir en kilolibras. Por lo tanto la Max Force en la unidad de RW son las klbf. Para una locomotora americana o inglesa, que ya mide en libras, es sencillo. Sólo se trata de dividir el esfuerzo de tracción máximo (el del arranque) por 1000. Si tenemos el valor como es habitual aquí en kilogramos, como sabemos que 1 Kg = 2.2045 lb, el esfuerzo de tracción máximo se obtiene de la siguiente forma: MF= Kg x 2.2045 / 1000. Para una locomotora con un máximo esfuerzo de tracción de 8.800 kg como la Hunslet de la Camocha sería:
MF = 8.800 x 2.2045 / 1000 = 19,39 klbf. Para una 251 de Renfe, para un valor de 35.600 kgs sería: MF = 35.600 x 2.2045 / 1000 = 78,39 klbf.
Como vemos, en el listado hay valores pequeños, como el de la Little John, establecido en 3, que son 3.000 libras. o lo que es lo mismo 1.300 kgs. Me parece un poco poco, aunque no tengo los datos de la locomotora real. Una 020T de Renfe pequeña, como las albardas de Triano, tienen una potencia de 2.830 kg, aunque es cierto que la más pequeña de vía ancha que ha habido, las 020 del Urbano de Jerez tenían sólo 930 kg. Podemos admitir el valor como válido, pero no su extrapolación, como se ha hecho, en la 021 "Sir Derek" que usan los mismos, aunque sea una locomotora mucho mayor, sin duda porque copia de aquella. En sentido contrario, para otra Saddle Tank idéntica, se establecen sin embargo un valor de 15 de esfuerzo de tracción, lo que serían nada menos que unos 6.818 kg, que es le que tenían locomotoras 230 grandes de Renfe...
Curvas
Este es un caso curioso que demuestra que las físicas de RW se diseñaron pensando en el vapor. En este tipo de tracción las relaciones de esfuerzo de tracción con velocidad y cambio de marcha se hacen sobre el valor 1 para potencia máxima y reduciendo el mismo en proporción.
Sin embargo en las diesel y eléctricas en las curvas donde se emplea el Tractive Effort, no se usa este sistema de proporcionalidad sino de valores absolutos, pero además, para liarla más, parten de un valor de esfuerzo de tracción máximo que no está como en en blueprint en klbf sino en kN...
En resumen:
Max Power:
Potencia máxima de la locomotora en HP
Max Force:
Esfuerzo de tracción máximo en el arranque en kilolibras. La fórmula para hallarlo desde kilogramos es MF = Kg x 2,2045 / 1000
Curvas
En vapor el valor máximo de ET es siempre 1 y se reduce en proporción.
En diesel y eléctricas el valor máximo de las curvas es el mismo de la Max Force, es decir el esfuerzo de tracción máximo, pero en kN, hay que dividir la MF que tenemos en klbf entre 225 para obtener el valor en kN, o lo que es lo mismo ET = MF (en klbf) /225. Si partimos de kilogramos ET = MF (en kg) x 9,8 / 1000.
Otros datos:
Max continuous force: Esfuerzo de tracción continuo. Suele ser un valor conocido, pero si no lo es, puede usarse aproximadamente el 60% del esfuerzo de tracción (Max force) que se ha puesto como aquí en kilolibras..
Max power at rail: Es la fuerza que se puede usar para traccionar trenes una vez descontadas las pérdidas por otros sistemas, resistencia a la tracción, etc. RW recomienda valores del 70 u 80 % del valor de Max Power, pero me parece mucha pérdida. Pondremos el 90% del valor de MP en caballos.
Saludos:
Javier.-
- Adjuntos
-
- eds120107_jfl.jpg (50.92 KiB) Visto 19828 veces


